|
Yellow Duration for a Traffic Signal
Contrast between Practice and What is Required
|
Driver or Vehicle Characteristic
|
NCDOT Yellow Light Specification
Practice
|
Passenger Car
What is Required
|
Commercial Vehicles
What is Required
|
|
|

|

|
|
|
Perception
Reaction Time
|
|
|
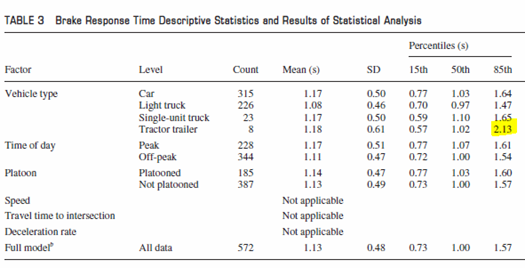
1.0 to 5.0
Seconds
|
|
|
|
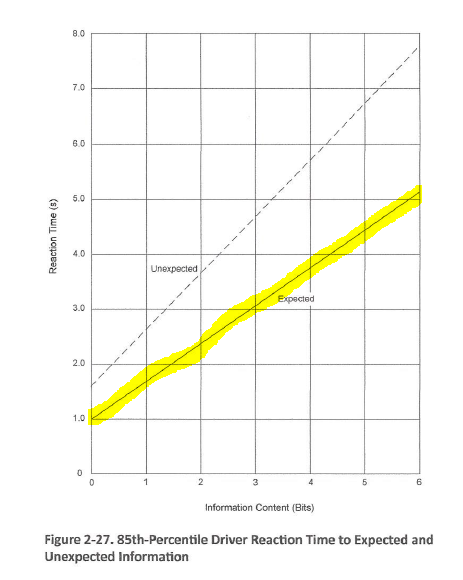
AASHTO
Green Book 2011, page 2-41.
The more information content the driver has to deal with near or
at the intersection, the more reaction time the driver needs to deal with
it.
|
|
|
|
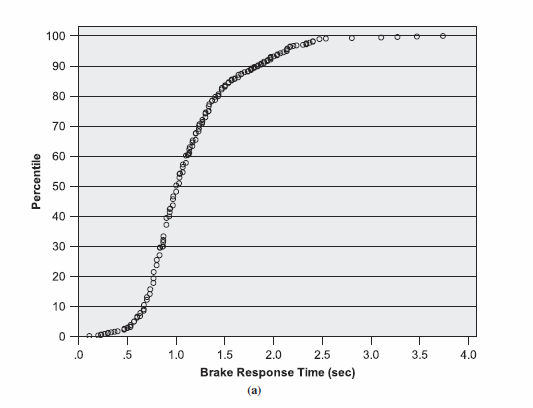
The 85th percentile perception-reaction
time is 1.57 seconds. Setting the
perception reaction time to 1.57 seconds excludes a large predictable set
of drivers. Many sources simply recommend
a 2.5 second minimum.
Gates, Dilemma Zone Driver Behavior as a Function of
Vehicle Type, Time of Day and Platooning, Transportation Research Record: Journal of
the Transportation Research Board, No. 2149, Transportation Research
Board of the National Academies, Washington, D.C., 2010, .p.
87.
|
|
|
|
Transportation
Research Institute, Oregon State Univ, 2007, p
8
|
|
|
|
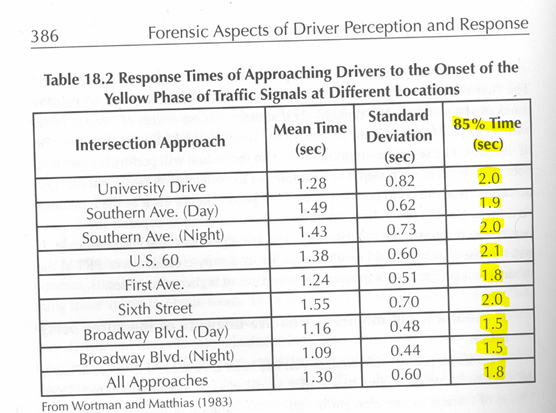
Olson,
Forensic Aspects of Driver Perception and Response, 2010, p. 386. The standard deviations are half the
range of values. That means there
are as many people responding in 0.6 seconds as 1.0 seconds as 1.4
seconds.
|
|

|
|
Transportation
Research Board, Wisconsin, 2007, page 21
|
|
|
2.2 Seconds Minimum
|
|
|
|
Gates,
Dilemma Zone Driver Behavior as a Function of Vehicle Type, Time of Day
and Platooning, Transportation
Research Record: Journal of the Transportation Research Board, No. 2149, Transportation Research
Board of the National Academies, Washington, D.C., 2010, p. 88.
|
|
|
Air Brake
Lag Time
|
|
|
|
|
Deceleration
|
|
11.2 ft/s2
|
|

|
|
NC
DOT Spec Sheet 5-2-2, Sheet 4 of 4
The NCDOT uses the wrong value for deceleration. 11.2 ft/s2
is only used in the context of emergency
braking. 10 ft/s2
is the median deceleration rate for normal braking.
|
|

|
|
AASHTO
Green Book, 2011, p3-3 Engineers
define the stopping sight distance in the context of emergencies. For emergency braking, 11.2 ft/s2 is the 90th percentile
deceleration rate. 90 percent of
vehicles will decelerate more rapidly than 11.2 ft/s2
when faced with an emergency.
11.2 ft/s2 is a “comfortable
deceleration for most drivers” but only in case of an emergency. Otherwise drivers expect to decelerate less aggressively. Intersection stopping distance and
deceleration, not stopping sight distance and deceleration, are the
values to use for an expected stopping event. See Intersection Stopping Distances at
the column to the right.
|
|

|
|
North
Carolina NCSITE, p 5 NCDOT
treats commercial vehicles as if they are passenger cars.
|
|
|
|
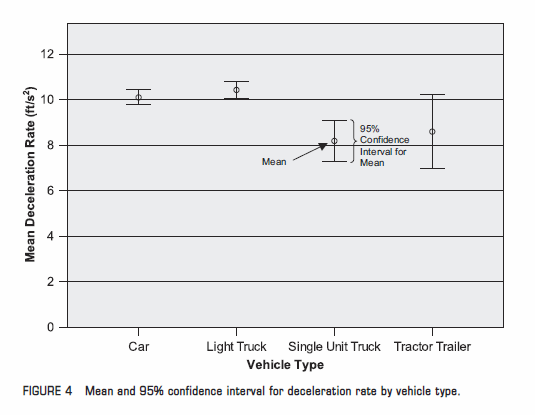
8.0 ft/s2 Maximum
|
|
|
|
Comparison between passenger cars and
commercial trucks.
Gates,
Dilemma Zone Driver Behavior as a Function of Vehicle Type, Time of Day
and Platooning, Transportation
Research Record: Journal of the Transportation Research Board, No. 2149, Transportation Research
Board of the National Academies, Washington, D.C., 2010, p.
91.
|
|

|
|
Gates,
Dilemma Zone Driver Behavior as a Function of Vehicle Type, Time of Day
and Platooning, Transportation
Research Record: Journal of the Transportation Research Board, No. 2149, Transportation Research
Board of the National Academies, Washington, D.C., 2010, pp. 84–93.p.
84
|
|

|
|
Maryland
Title 11 DOT, Subtitle 4, Ch 14. Traffic Signal Control Monitoring
|
|
|
|
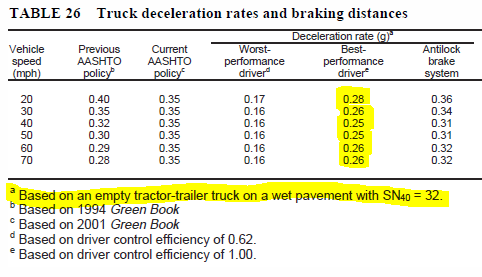
NCHRP
505, p. 48 0.25g = 0.25 * 32.2 ft/s2 = 8.0 ft/s2
These are maximum deceleration rates a truck
driver can do on a wet pavement in any situation. The comfortable rates will be less
than these.
|
|

|
|
USDOT, Effects of Deceleration on Live Human
Subjects, 1977, p 1, 0.23g =
0.23 * 32.2 ft/s2 = 7.4 ft/s2 The deceleration rate of transit
commercial vehicles, like school and public buses, are capped by the
position of their human occupants.
|
|

|
|
North
Carolina School Bus Drivers Handbook, 2014, p. 15
|
|
|
Approach
Speed
|
|
Speed Limit
Maximum
|
|

|
|
NC
DOT Spec Sheet 5-2-2, Sheet 4 of 4.
The NCDOT defaults “v” to the speed limit. Because the spec does not mandate that
the engineer use the 85th percentile speed, the engineer rarely
goes out of his way to perform the speed study. The spec incites the engineer to be
reactive, not proactive.
The NCDOT measures “v” at the intersection stop
bar. This is an egregious error
against physics. Physics mandates
the engineer to measure “v” at the critical distance upstream from the
intersection. See Equation for Duration of Yellow Light,
below, for the equation of the critical distance. On a 45 mph level road, the critical
distance is about 300 feet upstream from the intersection stop bar.
The NCDOT spec allows the engineer to set “v” to a
value less than the speed limit. When
the engineer sets “v” below the
speed limit, the engineer creates a type 1 dilemma zone for vehicles
approaching the intersection at speed “v” or greater. That means that the engineer will
force drivers approaching at speeds greater than “v” to run a red
light. Because speeds greater
than “v” include the legal speed limit, the engineer sets a trap for the
motorist. The engineer will force
honest citizens to run a red light.
|
|

|
|
Deposition
of David Spencer, p. 78.
Spencer does not know that the 85th percentile is that speed
of freely-flowing traffic
measured at the critical distance, not the speed of impeded traffic measured
at the intersection.
|
|
|
85th
Percentile, Speed Limit Minimum
|
|

|
|
ITE,
Traffic Engineering Handbook, 2010, p. 101.
The speeds engineers place on speed limit signs and
input into the yellow light formula is a topic unto itself. The incompatibility between properly-engineered
speeds and man-made laws is always present.
A basic rule of engineering is to accommodate human
behavior. When the majority of
traffic travels above the speed limit, the engineer should accommodate
the majority. An engineer should
set the yellow light using that higher speed, thus lengthening the yellow
thus making the intersection safer.
The engineer cannot set “v” below the speed limit for that would
effectively remove the required stopping distance from the legally-moving
driver, force him to break the law and possibly force him to crash.
Speed limits themselves are supposed to be set to the
85th percentile speed but physical limitations and city
ordinances control what numbers appear on the speed limit sign. For example, even though the 85th
percentile speed changes between rush hour and midnight, only one speed
limit value can be appear on a sign.
The sign cannot say “35 mph” from 7 AM to 9 AM then change to “55
mph” from 11 PM to 5 AM. Also many cities in North Carolina have
ordinances which require speed limits confined to increments of 10 mph;
for example, 5, 15, 25, 35, 45 and
55 mph. And so the traffic
engineer picks the lowest closest speed but the speed may be too slow—too
unnatural for the motorist.
Imagine a 10 mph sign on Interstate 40. How dangerous would such a sign make
the Interstate?
|
|
Approach Speed is the Least of Concerns
Many traffic engineers are aware of setting yellows
with the 85th percentile speed. Many anti-red light camera
organizations focus on the 85th percentile speed. In the end, however, traffic engineers
not adopting the 85th percentile speed is the least of the
engineers’ transgressions. While
a driver can control his speed, a driver cannot control the laws of
physics, how fast his vehicle can decelerate or how fast his brain can
react to information.
Nonetheless, a properly set 85th
percentile speed will increase the yellow by about 1 second.
|
|
|
85th
Percentile, Speed Limit Minimum
|
|
|
Equation for Duration of Yellow Light
|
|
Straight-Through Unimpeded
Movement Equation
(Equation shorts yellow time by several seconds for movements other
than straight-through unimpeded traffic.)
|
|

|
|
NC
DOT Spec Sheet 5-2-2, Sheet 4 of 4.
The physics of this formula models only straight-through traffic
but the NCDOT applies it to all traffic movements.
The formula offers the driver a mutually exclusive
choice between stop and go full speed.
If the driver must proceed because he is too close to the
intersection, the formula requires him to go full speed “v” toward and
into the intersection. The formula
does not allow him to slow down.
The formula does allow to slow down to turn, to slow down to avoid
cars entering or egressing from nearby business, to slow down to avoid a
hazard, or to slow down just to be cautious.
|
|

|
|
MUTCD,
2009, p. 489. The MUTCD caps the yellow change
interval to 6 seconds; but turning movements can take 6 – 9 seconds
easily.
|
|

|
|
North
Carolina NCSITE, p 5 NCDOT
treats commercial vehicles as if they are passenger cars. But unlike passenger cars, commercial
vehicles have air brakes.
|
|

|
|
North
Carolina NCSITE, p 5 The
formula for straight-through movement traffic is different than left
turning vehicles.
|
|

|
|
NC
DOT Spec Sheet 5-2-2, Sheet 4 of 4.
By NCDOT misunderstanding the formula, for any left turn
approaching vehicle, 1) even if the vehicle is approaching at 45 mph the
NCDOT gives it the stopping distance of a 20 mph vehicle. Here the NCDOT ignores the law of
momentum. The NCDOT ignores the
tightly-coupled relationship between speed, distance and time. Regardless of lane in which the car
travels, the car’s initial speed dictates his stopping distance. A given speed limit applies to all
lanes of traffic, to cars preparing to enter the left turn bay or that
have already entered the left turn bay.
2) The NCDOT exacerbates the
time problem for the driver when he decides to proceed. Traversing this fixed distance while
decelerating for turning, increases not decreases, his needed time for
the light to remain yellow. Left turn yellows must be longer, not
shorter, than the straight-through yellows.
|
|
|
Equations for Straight, Turning,
Impeded and General Movements
|
|
Formula for Unimpeded Straight-Through Movement
Traffic
(Gazis,
Herman, Maradudin, ITE)
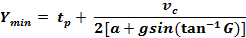
|
|
Formula for Turning Traffic (Left,
Right, U)
(Liu,
et al., American Society of Civil Engineers, Eq
13)
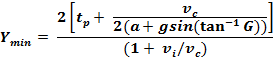
|
|
Formula for Impeded Traffic
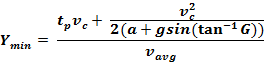
|
|
General Formula That Works for all
Traffic
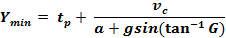
|
|
Stopping Distance (or critical distance) Formula. vc is measured at distance c:
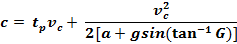
|
|
Derivation of Above Formulas from
Newton’s Second Law of Motion.
(G = grade, g = earth’s
gravitational acceleration = 32.2 ft/s2. See derivation).
The general formula and the formula
for turning traffic compute yellow times several seconds longer than practice. For example, the general formula for
a typical 45 mph road computes a yellow change interval about 3 seconds
longer than the straight-through formula.
|
|
|
Equations for Straight, Turning,
Impeded and General Movements
Including Air Brake Lag Time
|
|
Formula for Unimpeded Straight-Through Movement
Traffic
(Gazis,
Herman, Maradudin, ITE)
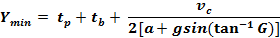
|
|
Formula for Turning Traffic (Left,
Right, U)
(Liu,
et al., American Society of Civil Engineers, Eq
13)
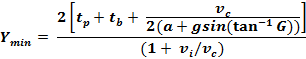
|
|
Formula for Impeded Traffic
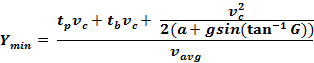
|
|
General Formula That Works For all
Traffic
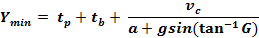
|
|
Stopping Distance (or critical distance) Formula. vc is measured at distance c:
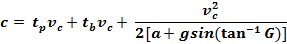
|
|
Derivation of Above Formulas from
Newton’s Second Law of Motion.
(G = grade, g =
earth’s gravitational acceleration = 32.2 ft/s2,
tb = air brake lag time. See derivation).
The general formula and the formula
for turning traffic compute yellow times several seconds longer than practice. For example, the general formula for
a typical 45 mph road computes a yellow change interval about 5 seconds
longer than the straight-through formula.
|
|
|
POLICE LINE
|
POLICE
LINE POLICE LINE POLICE LINE POLICE LINE POLICE LINE
|
POLICE LINE POLICE LINE POLICE LINE
POLICE LINE POLICE LINE POLICE
|
POLICE LINE POLICE LINE POLICE LINE
POLICE
LINE POLICE LINE
|
|
Law
Enforcement
|
|
Zero Tolerance
|
|
The moment the light turns red, law enforcement can
ticket the driver.
Police assume that engineers time the traffic signals
correctly. Yet the police are not
aware that engineers ignore the needs of commercial vehicles. The police are not aware that
engineers do not consider physics and human factors correctly in the
yellow light formula. The police
are not aware that engineers use the wrong formula and plug the wrong
numbers into the formula.
The police are
aware of the three “E”s: Engineering. Education. Enforcement. One cannot have the latter without the
former. But police rely on
engineers to tell them whether the engineering is correct. Engineers do not inform enforcement of
their decision to make honest people run red lights. Engineers do not confess to the law
enforcement that they do not know the physics of their own formula. Engineers do not know how to compute
the tolerance in their yellow light calculations in order to inform law
enforcement of the leniency the law must grant the driver.
The police are trained to ticket drivers, not traffic
engineers.
Engineers are happy to perpetuate this training.
|
|

|
|
TxDOT Report 0-4273-2, 2003, pp, 27-28.
Texas’ report guides traffic engineers to set the
left turn yellow so that traffic can move most efficiently. The authors of the report poll
engineering professionals, asking them what parameters they consider most
important. The report lists those
parameters by priority.
It is crucial for law enforcement to understand that
engineers rank the legal motion of traffic as 7th
priority. It is crucial for law
enforcement to understand that the legal motion of traffic competes with
the engineers’ primary goal: efficient traffic flow. Engineers gladly sacrifice a driver’s
ability to traverse an intersection legally if it means a dozen cars can
make it through the intersection in a given signal cycle. It is standard practice for engineers
to knowingly make millions of drivers to run red lights in order to
attain level of service (LOS) goals.
An intersection with a low LOS makes the engineer look bad.
It is crucial for law enforcement to know that the
safety of traffic does not automatically imply the legal motion of
traffic and vice-versa.
The attitude
traffic engineers take when it comes to knowingly making drivers run red
lights is exemplified in these exerts from legal depositions of North
Carolina DOT’s traffic engineers (NCDOT):
|
|

|
|
Deposition of Dr. Joseph Hummer, pp. 108-109.
|
|

|
|
Deposition
of Lisa Moon, p 63. This is
Moon’s statement after shown a graph depicting a dramatic spike
in the red light running violations at NB Kildaire
Farms Road at Cary Parkway after the North Carolina DOT shortened its
left turn yellow from 4 to 3 seconds.
|
|

|
|
Deposition
of Dr. Joseph Hummer, pp. 63.
After Hummer works the algebra backwards and discovers that the
NCDOT expects all drivers approaching in the left turn lane to be
approaching at 23 mph or less, Hummer has to consult a lawyer to tell him
going 45 mph in a 45 mph speed zone is legal.
Law
enforcement assumes that traffic engineers set traffic signal timing
correctly. But traffic engineers
do not know what “correct” is.
They set traffic signal timing to “spec” but do not question the
spec. They do not understand the
spec and do not know if it actually properly handles physics:
|
|

|
|
Deposition
of Lisa Moon, p. 27.
|
|

|
|
Deposition
of Lisa Moon, p. 22. Physics
is not the practice of the NCDOT.
|
|

|
|
Deposition
of Lisa Moon, p. 22. Moon,
though an engineer in charge of the motion of traffic at 1000
intersections in North Carolina, could not name a single one of
Newton’s Laws of Motion. Paul
Stam, the attorney, had to help her out.
Moon believes that F = ma can only be used in a “very limited
vacuumed world.”
None of the professional engineers that the Town of
Cary used as expert witnesses could recite Newton’s Laws of Motion.
|
|

|
|
Deposition
of Lisa Moon, p 37. The NCDOT
measures “v” at the stop bar as 20 mph for left-turning lanes, unaware
that the formula does not apply to left-turning lanes and unaware that v
is measured at the critical distance, not at the stop bar. On a 45 mph in North Carolina, the
critical distance is about 294 feet upstream from the intersection.
Many States, including California and Virginia, make
the same mistake for “v.”
|
|

|
|
Deposition
of Daren Marceau, p. 112.
When shown the general equation for the yellow change interval,
Mr. Marceau did not recognize as such.
He though it was a new equation.
A page later, Marceau understood that the new equation would add
several seconds to the yellow.
Several seconds longer is what is required for turning movements
but Marceau dismissed the very equation from which his own formula is
derived.
|
|
|
2 to 4 Seconds Tolerance
(In addition to using the correct formula.)
|
|

|
|
Gazis,
et al, The Problem with the Amber Signal Light in Traffic Flow, p.
112. These three physicists invented the
straight-through unimpeded yellow light formula traffic engineers use today.
|
|

|
|
Gazis,
et al, The Problem with the Amber Signal Light in Traffic Flow, p. 129. The formula they invented does not apply
to two closely spaced traffic lights, nor turning, unless the turning is
done at a slow speed.
Today’s traffic engineers use the formula as a
one-size-fits-all.
|
|
"The formula actually violates the laws of
physics for certain types of motions, traffic motions," said
Ceccarelli.
Ceccarelli said the Department of Transportation's
formula for yellow lights only works for cars going straight through the
light, and only cars that stay at or above the speed limit.
"It
doesn't apply to any type of traffic movement that has to decelerate into
the intersection," said Ceccarelli.
To check Ceccarelli's
math, the I-Team went to the source. Alexei Maradudin is now a physics
professor at the University of California - Irvine. In 1960, he came up
with the root formula, which is still used by the DOT.
"That's
correct. We did not, in our analysis consider turns; either left and
turns or right hand turns," said Maradudin. "It was really
straight through the intersection dynamics that we considered."
That formula made it into the traffic engineering
handbook, and has been used, or misused, as Ceccarelli puts it in North
Carolina, and across the country ever since.
"It
causes lots and lots of people to run red lights, involuntarily," he
said.
According to
Ceccarelli, yellow lights should generally be three to four seconds
longer. So, why are they set as they are? Based on a flawed formula
written 55 years ago?
"I
think that's a question that should be addressed to the Departments of
Transportation," said Maradudin.
|
|
ABC, WTVD, Channel 11 interview with Dr.
Maradudin and Mr. Ceccarelli., May 6, 2014
|
|
Error propagation.
The values for perception reaction time, deceleration rate,
approach speed and grade of road are not idyllic constants. The values have a range of equally valid
values or at least a standard deviation. Therefore the yellow change interval,
calculated from this imprecise values, is also imprecise. The measure of the yellow’s
impreciseness is calculated using error propagation.
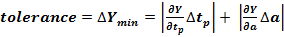 . . . . . .
Tolerance Required for Unimpeded Straight-Through
Movement Traffic
Assume the error in vc and G are negligible. The tolerance, T, required for this
type of traffic under these ideal conditions is about 2.3 seconds.
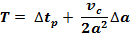
Tolerance Required for Turning Traffic
Assume the error in vc and G are negligible. The tolerance required for this type
of traffic, using the turning formula, under ideal conditions are 3.4
seconds.
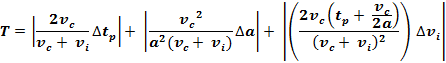
|
|
Error propagation.
|
|
|
Yellow Duration for a Traffic Signal
Emergency Condition:
Car Unexpectedly Crossing Your Path
Contrast between Practice and What is Required
|
Driver or Vehicle Characteristic
|
NCDOT Yellow Light Specification
Practice
The NCDOT practice does not accommodate hazards
occurring in or nearby the intersection.
NCDOT’s yellow change interval requires a driver who can no longer
stop comfortably, to proceed at the speed limit or more without slowing
down. Not only does the practice
forbid movements like turning, but also the practice compels the driver to
continue proceeding to the intersection at full speed without regard for
potential hazards. The driver may
see hazards, like cars turning left crossing his path in front of him, but
if he slows down for them, he risks certain hazard by running a red light.
|
Passenger Car
What is Required
|
Commercial Vehicles
What is Required
|
|
|

|

|
|
|
Perception
Reaction
Time
|
|
1.5 Seconds
|
|

|
|
NC
DOT Spec Sheet 5-2-2, Sheet 4 of 4
The NCDOT formula does not consider emergencies occurring within
or near the intersection. It
takes about 1 second more for a driver to perceive and react to a hazard.
|
|
|
1.8 to 8.0
Seconds
|
|
|
|
AASHTO
Green Book 2011, page 2-41.
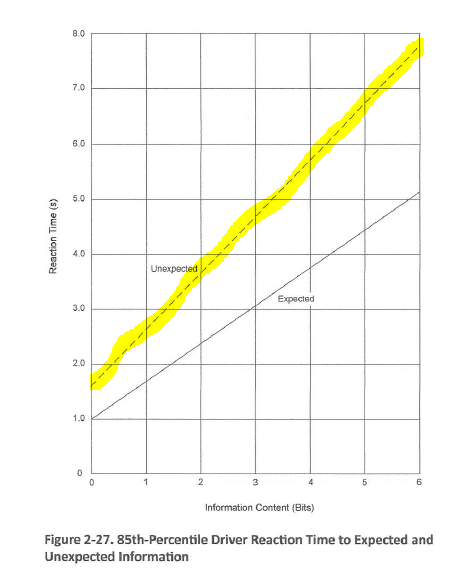
The more information content the driver has to deal with near or
at the intersection, the more complex the intersection.
|
|
|
|
Air Brake
Lag Time
|
|
|
|
|
Deceleration
|
|
11.2 ft/s2
|
|

|
|
NC
DOT Spec Sheet 5-2-2, Sheet 4 of 4.
The NCDOT formula
does not consider emergencies occurring within or near the intersection.
The formula offers the driver a mutually exclusive
choice between stop and go full speed.
If the driver must proceed because he is too close to the
intersection, the formula does not allow him to slow down for any
reason. The formula does allow to
slow down to turn, to slow down to avoid cars entering or egressing from
nearby business, to slow down to avoid a hazard, or to slow down just to
be cautious.
|
|
|
11.2 ft/s2
is the 90th Percentile Emergency Braking Rate
But for the yellow
light, the deceleration must be the lower normal deceleration rate 10
ft/s2. The yellow light cannot be timed such
that it expects a car to emergency brake.
|
|

|
|
AASHTO
Green Book, 2011, p3-3
|
|
|
8.0 ft/s2
is Maximum a Truck can do on Wet Pavement
|
|

|
|
NCHRP
505, p. 48 0.25g = 0.25 * 32.2 ft/s2 = 8.0 ft/s2
Which is the best a truck driver can do on a
wet pavement in any situation.
|
|
|
Equation
|
|
Straight-Through Unimpeded
Movement Equation
|
|

|
|
NC
DOT Spec Sheet 5-2-2, Sheet 4 of 4
The physics of this formula models only straight-through traffic
but the NCDOT applies it to all traffic movements.
The formula offers the driver a mutually exclusive
choice between stop and go full speed.
If the driver must proceed because he is too close to the
intersection, the formula does not allow him to slow down to turn, to
slow down to avoid cars entering or egressing from nearby business, to
slow down to avoid a hazard, or to slow down for any reason.
|
|

|
|
MUTCD,
2009, p. 489. The MUTCD caps the yellow change
interval to 6 seconds; but turning and/or avoidance movements can easily
require up to 10 seconds.
|
|
|
General Formula Only
|
|
General Formula That Works For all Non-Commercial
Traffic, including Avoidance Maneuvers
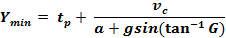
|
|
Stopping Distance (or critical distance) for all
Non-Commercial Traffic, Formula. vc is measured at distance c:
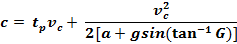
|
|
Derivation of Above Formulas from
Newton’s Second Law of Motion.
(G = grade, g =
earth’s gravitational acceleration = 32.2 ft/s2. See derivation).
The general formula allows drivers
to slow down on route to the intersection without running a red
light. The general formula
produces yellow times several
seconds longer than practice.
For example, the general formula for a typical 45 mph road
computes a yellow change interval about 3 seconds longer than the
straight-through formula.
|
|
|
General Formula Only which includes
Air Brake Lag Time
|
|
General Formula That Works For all
Traffic, including Avoidance Maneuvers
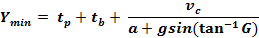
|
|
Stopping Distance (or critical distance) Formula. vc is measured at distance c:
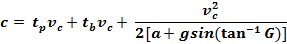
|
|
Derivation of Above Formulas from
Newton’s Second Law of Motion.
(G = grade, g =
earth’s gravitational acceleration = 32.2 ft/s2,
tb = air brake lag time. See derivation).
The general formula allows drivers
to slow down on route to the intersection without running a red
light. The general formula
produces yellow times several
seconds longer than practice.
For example, the general formula for a typical 45 mph road
computes a yellow change interval about 5 seconds longer than the
straight-through formula.
|
|
|